|
|
|
Другие доказательства
|
Доказательство Евклида
Это доказательство было приведено Евклидом в его "Началах".
По свидетельству Прокла (Византия), оно придумано самим Евклидом.
Доказательство Евклида приведено в предложении 47 первой книги "Начал".
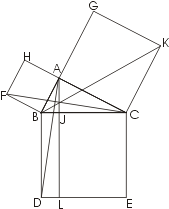
На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты
и доказывается, что прямоугольник BJLD равновелик квадрату ABFH,
а прямоугольник ICEL - квадрату АСКС. Тогда сумма квадратов
на катетах будет равна квадрату на гипотенузе.
В самом деле, треугольники ABD и
BFC равны по двум сторонам и углу между ними:
FB = AB, BC = BD
РFBC = d + РABC = РABD
Но SABD = 1/2 S BJLD,
так как у треугольника ABD и прямоугольника BJLD
общее основание BD и общая высота LD.
Аналогично
SFBC=1\2S
ABFH
(BF-общее основание, АВ-общая высота).
Отсюда, учитывая, что
SABD=SFBC,
имеем
SBJLD=SABFH.
Аналогично, используя равенство треугольников ВСК и АСЕ, доказывается, что
SJCEL=SACKG.
Итак, SABFH+SACKG=
SBJLD+SJCEL=
SBCED,
что и требовалось доказать.
|
|
|
Упрощенное доказательство Евклида
Как в доказательствах методом разложения, так и при
доказательстве евклидового типа можно исходить из любого
расположения квадратов. Иногда при этом удается достигнуть
упрощений.
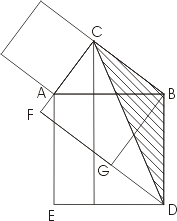
Пусть квадрат,построенный на одном из катетов
(на рисунке это квадрат,построенный на большем катете),
расположен с той же стороны катета, что и сам треугольник.
Тогда продолжение противоположной катету стороны этого квадрата
проходит через вершину квадрата, построенного на гипотенузе.
Доказательство в этом случае оказывается совсем простым, т. к.
здесь достаточно сравнить площади интересующих нас фигур с
площадью одного треугольника(он заштрихован) - площадь этого
треугольника равна половине площади квадрата и одновременно половине
площади прямоугольника
|
|
Доказательство Хоукинсa.
Приведем еще одно доказательство, которое имеет вычислительный характер,
однако сильно отличается от всех предыдущих.
Оно опубликовано англичанином Хоукинсом в 1909 году; было ли оно известно до этого-
трудно сказать.
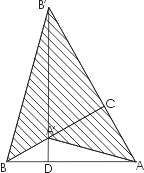
Прямоугольный треугольник ABC с прямым углом C повернем на 90° так,
чтобы он занял положение A'CB'. Продолжим гипотенузу A'В' за точку A' до пересечения
с линией АВ в точке D. Отрезок В'D будет высотой треугольника В'АВ. Рассмотрим теперь
заштрихованный четырехугольник A'АВ'В . Его можно разложить на два равнобедренных
треугольника САA' и СВВ' (или на два треугольника A'В'А и A'В'В).
SCAA'=b²/2
SCBB'=a²/2
SA'AB'B=(a²+b²)/2
Треугольники A'В'А и A'В'В имеют общее основание с и высоты DA и DB, поэтому :
SA'AB'B=c*DA/2+ c*DB/2=c(DA+DB)/2=c²/2
Сравнивая два полученных выражения для площади, получим:
a²+b²=c²
Теорема доказана.
|
 |
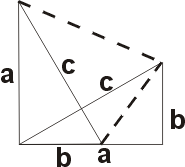
Доказательство Вальдхейма.
Это доказательство также имеет вычислительный характер. Можно использовать рисунки для доказательства
основанного на вычислении площадей двумя способами.
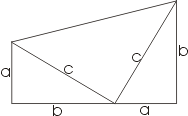
Для того чтобы доказать теорему пользуясь первым рисунком достаточно только выразить площадь
трапеции двумя путями.
Sтрапеции=(a+b)²/2
Sтрапеции=a²b²+c²/2
При
равнивая правые части получим:
a²+b²=c²
Теорема доказана.
|
 |
|
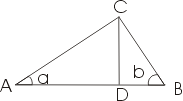
Доказательство основанное на теории подобия.
В прямоугольном треугольника АВС проведем из вершины прямого
угла высоту CD; тогда треугольник разобьется на два треугольника,
также являющихся прямоугольными.
Полученные треугольники будут подобны
друг другу и исходному треугольнику. Это легко доказать, пользуясь
первым признаком подобия(по двум углам).
В самом деле, сразу видно что, кроме прямого угла, треугольники АВС и ACD имеют общий угол a,
треугольники CBD и АВС - общий угол b. То, что малые треугольники
также подобны друг другу, следует из того, что каждый из них подобен
большому треугольнику. Впрочем, это можно установить и непосредственно.
|
|
|
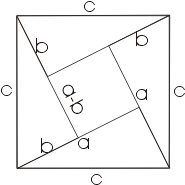
Доказательство индийского математика Басхары изображено на рисунке.
В пояснение к нему он написал только одну строчку: "Смотри!". Ученые
считают, что он выражал площадь квадрата ,построенного на гипотенузе,
как сумму площадей треугольников (4ab/2) и площадь квадрата (a-b)².
Следовательно:
c²=4ab/2+(a-b)²
c=2ab+a²-2ab+b²
c²=a²+b²
Теорема доказана.
|
|
|
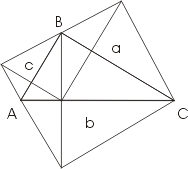
Луночки Гиппократа
Для того, чтобы доказать теорему о гиппократовых луночках,
докажем следующее предложение: Если на катетах и на гипотенузе
прямоугольного треугольника построены какие угодно подобные между
собой фигуры Fa, Fb, Fc, так, что катеты и гипотенуза являются
сходственными отрезками этих фигур, то имеет место равенство:
Fa+Fb=Fc.
Для доказательства воспользуемся
следующей теоремой из
теории подобия: площади подобных многоугольников относятся как
квадраты сходственных сторон.
Если через Fa, Fb, Fc обозначить площади
подобных многоугольников, построенных на катетах
a, b и гипотенузе
с прямоугольного треугольника, то согласно вспомогательной теореме
можно написать:
Fa/Fb/Fc=a²/b²/c².
Эта пропорция означает,что можно
найти число k (коэффицент пропорциональности) такое, что
Fa=ka² Fb=kb² Fc=kc²..
Умножив обе части равенства на k и принимая во внимание предыдущие
равенства, получим:
Fa+Fb=Fc.
Если равенство Fa+Fb=Fc имеет место хотя
бы для одной тройки подобных между собой многоугольников, построенных
на катетах и на гипотенузе прямоугольного треугольника АВС так, что АС,
ВС и АВ есть сходственные отрезки этих многоугольников, то
ka²+kb²=kc²
(где k имеет какое-то определенное значение, зависящее от выбора
многоугольников, - нам совершенно не важно, какое именно). Но отсюда
вытекает, что
а²+b²=с²,
а это влечет за собой тот факт,что равенство
Fa+Fb=Fc выполняется для любых построенных на сторонах прямоугольного
треугольника подобных многоугольников, в частности, и для квадратов.
|
|
|
Познакомимся с одним интересным предложением, которое встречается во
многих учебниках геометрии под названием теоремы о Гиппократовых
луночках.
Гиппократ Хиосский (вторая половина пятого века до н. э.,
Афины) занимался квадратурой луночек. Он называл луночкой часть
плоскости, ограниченную двумя дугами окружностей. Наше предложение в
том виде, как оно будет здесь сформулировано, не встречается у самого
Гипократа, который нашел квадратуру только для некоторых луночек. Во
всей общности теорему доказал араб Ибн Альхаитам:
"Если на гипотенузе прямоугольного треугольника как на диаметре описать
полуокружность, лежащую с той же стороны гипотенузы, что и сам
треугольник, то она пройдет через вершину прямого угла." Эту теорему
греки приписывали Фалесу Милетскому, но в действительности ее знали
еще древние вавилоняне.
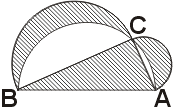
Опишем две полуокружности на катетах так,
как указано на рисунке, тогда получатся две луночки.
Пусть Ка,Кв,Кс- площади полукругов, построенных на катетах и гипотенузе.
Согласно теореме, рассмотренной ранее, имеем:
Ка+Кb=Кс.
Этот же результат можно получить, умножив обе части равенства
А²+В²=С² на π/8.
В самом деле, равенство
(π/8)А+(π/8)В=(π/8)С
означает,что площадь полукруга С диаметром с равна сумме площадей
двух других полукругов, с диаметрами a и b. Если мы отнимем те же
части(на рисунке они не заштрихованы )как от полукруга,построенного
на гипотенузе, так и от полукругов, построенных на катетах, то, вследствие
только что доказанной теоремы, получим, что сумма площадей луночек
равна площади треугольника.
|
|
Векторное док-во
Пусть АВС - прямоугольный треугольник с прямым углом при вершине С,
построенный на векторах. Тогда справедливо векторное равенство:b+c=a
откуда имеем
c = a - b
возводя обе части в квадрат, получим
c²=a²+b²-2ab
Так как a перпендикулярно b, то ab=0, откуда
c²=a²+b² или c²=a²+b²
Нами снова доказана теорема Пифагора.
Если треугольник АВС - произвольный, то та же формула дает т. н.
теорему косинусов, обобщающую теорему Пифагора.
|

|
|



